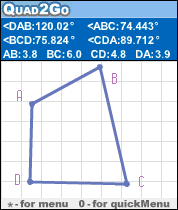
Quad2Go - Explorations з Quad2Go особливо підходять для 11-12-річних студентів. Навчання геометрії студентів цього віку фокусується на критичних ознак чотирикутників і ієрархічних відносин між ними. означає визначення критичних атрибутів і несуттєві атрибути навчання. Наприклад, & Quot; чотири сторони, & Quot; & Quot; дві пари паралельних сторін, & Quot; або & Quot; дві пари рівних протилежних кутів & Quot; є одними з найважливіших ознак паралелограма; & Quot; дві довгі сторони і дві короткі сторони & Quot; або & Quot; два гострих кутів і двох тупих кутів & Quot; є некритичні атрибути. Навчання в цьому сенсі означає навчитися аналізувати атрибути різних каре, щоб розрізняти їх критичних і некритичних атрибутів, а також вивчення ієрархії серед квадрациклів. Quad2Go дає багато прикладів випадковим чином побудованих квадрациклів. Кожен приклад може бути змінений шляхом перетягування або його вершини або сторони.
<Сильні> Особливості Quad2Go є зручним інструментом для вивчення чотирикутників шляхом створення прикладів, спостерігаючи й експериментуючи з прикладами з метою до формування узагальнених домисли. Точно так же до часто використовуваних динамічної геометрії Середовища (DGE), такі як геометричне Supposer, Кабрі Геометрія і геометр Альбом, Quad2Go пропонує геометричні об'єкти, інструменти для роботи з ними, а також інструменти вимірювання. Вона обмежена чотирикутників і будівництво діагоналей. Quad2Go дозволяє користувачам будувати, переглядати і перетворювати чотирикутника, сумісні з тими, побудованих з прямим краєм і компас, для вимірювання довжини, кути і площі, а також керувати будівництвом шляхом перетягування і перетворення його форму. Перетягування дозволяє змінювати форму шляхом прямого переказу частин його компонентів на екрані. Вчимося DGE тісно пов'язана з теоріями конструктивістського навчання, в яких сенс будується на основі активної участі учня.
<Сильні> Пропоновані заходи
Дослідження ієрархії квадрациклів
Використовуйте меню Форми для побудови паралелограми, повітряні змії, трапецій і ромбів.
В меню Quad2Go вибрати для перегляду паралелограми.Ось побудова паралелограма. Чому?
Можливо, ви отримаєте прямокутник в якості одного з паралелограмів? Чи згодні ви, що це прямокутник? Як ви думаєте, ви можете отримати прямокутник? Чому?
Під який вибір фігури ви б очікувати, щоб отримати квадрат? Чому?
Розвідка завдання про нестандартну класифікації
квадрат, ромб, і змій є квадрациклів, які поділяють наступну властивість: кут між їх діагоналей є прямим кутом. Квадроцикли з цією властивістю називаються orthodiagonal квадрациклів.
Відкрийте для себе інші спеціальні властивості цього класу квадрациклів.
Реалізація знань про трикутників
У будь-якому опуклому чотирикутнику дві діагоналі створити вісім трикутників. Для кожного типу даного чотирикутника:
Визначити 8 трикутників
Визначення 4 конгруентних трикутників; пояснити своє рішення.
Визначення 2 конгруентних трикутників; пояснити своє рішення.
Визначення подібних трикутників; пояснити своє рішення.
<Сильний> Що нового в цій версії:
& Мідот; малюнок економія
& Мідот; входять
& Мідот; переваги
& Мідот; Покращена графіка& Мідот; Виправлення помилок
Докладна інформація про додатки:
Версія: 0.84
Дата завантаження: 28 Apr 11
Розробник: Math4Mobile
Ліцензія: Безкоштовно
Популярність: 211
Розмір: 102 Kb







Коментар не знайдено